Welcome to the introduction to two-step equations, where you’ll learn to solve linear equations requiring two operations, essential for math and real-life problem-solving. This section provides foundational knowledge and practical examples to enhance your algebra skills.
1.1 What Are Two-Step Equations?
Two-step equations are algebraic expressions requiring two operations to solve for the variable. They involve combining or separating numbers using addition, subtraction, multiplication, or division. For example, an equation like (3x + 5 = 11) requires subtracting 5 and then dividing by 3 to find (x). These equations are fundamental in algebra, teaching students to apply inverse operations in sequence. Unlike one-step equations, two-step problems demand a deeper understanding of mathematical relationships and procedural steps. Mastering them builds a strong foundation for solving more complex equations in the future. They are widely used in worksheets and educational materials to enhance problem-solving skills.
1.2 Importance of Solving Two-Step Equations
Solving two-step equations is crucial for building foundational math skills, as it enhances problem-solving abilities and logical thinking. These equations require applying multiple operations, fostering a deeper understanding of algebraic concepts. Mastery of two-step equations prepares students for more complex math, such as quadratic equations and word problems. It also improves analytical skills, essential for real-world applications in science, finance, and everyday decision-making. By practicing two-step equations, learners develop patience and accuracy, which are vital for academic and professional success. This skill is a stepping stone to advanced math, making it indispensable for a strong educational foundation.

1.3 Brief Overview of the Worksheet

The worksheet on solving two-step equations is designed to help learners master algebraic problem-solving. It includes a variety of equations requiring two operations, such as addition, subtraction, multiplication, and division. The problems are structured to gradually increase in difficulty, ensuring a smooth learning curve. Each equation is presented clearly, with space for students to write their solutions. The worksheet also provides answers, allowing learners to check their work and identify areas for improvement. This resource is ideal for classroom use or independent practice, offering a comprehensive way to build confidence and fluency in solving two-step equations. It aligns with curriculum standards and supports long-term math skills development.

Understanding the Basics of Two-Step Equations
Two-step equations involve basic operations like addition, subtraction, multiplication, and division. They require two operations to isolate the variable, making them fundamental for building problem-solving skills in math.
2.1 Definition and Examples
A two-step equation is a linear equation that requires two operations to solve for the variable. It involves combining or separating quantities through addition, subtraction, multiplication, or division. For example, in the equation 2x + 3 = 7, the first step is subtracting 3 from both sides, and the second step is dividing by 2 to find x = 2. These equations are fundamental in algebra, as they introduce the concept of inverse operations and the importance of the order of operations. Mastering two-step equations builds a strong foundation for solving more complex problems in mathematics.
2.2 Key Concepts: Operations and Inverse Operations
Understanding operations and their inverses is crucial for solving two-step equations. Basic operations include addition, subtraction, multiplication, and division. Inverse operations “undo” each other, such as addition and subtraction or multiplication and division. For example, if an equation involves multiplying by 3, the inverse operation would be dividing by 3 to isolate the variable. Recognizing these relationships helps simplify equations step-by-step. Mastering inverse operations ensures accuracy in reversing operations to solve for variables effectively. This concept is foundational for algebraic problem-solving and real-world applications. By applying inverse operations strategically, you can systematically isolate variables and find solutions with confidence.

2.3 The Role of Order of Operations
The order of operations is a fundamental concept in solving two-step equations. It ensures that mathematical operations are performed in a consistent and logical sequence. In equations, operations like multiplication, division, addition, and subtraction must follow the PEMDAS rule (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). Neglecting this order can lead to incorrect solutions. For example, in an equation like 3x + 6 = 15, you must first divide by 3 after subtracting 6 to isolate x. Understanding and applying the order of operations correctly is essential for accurately solving two-step equations and building a strong foundation in algebra.
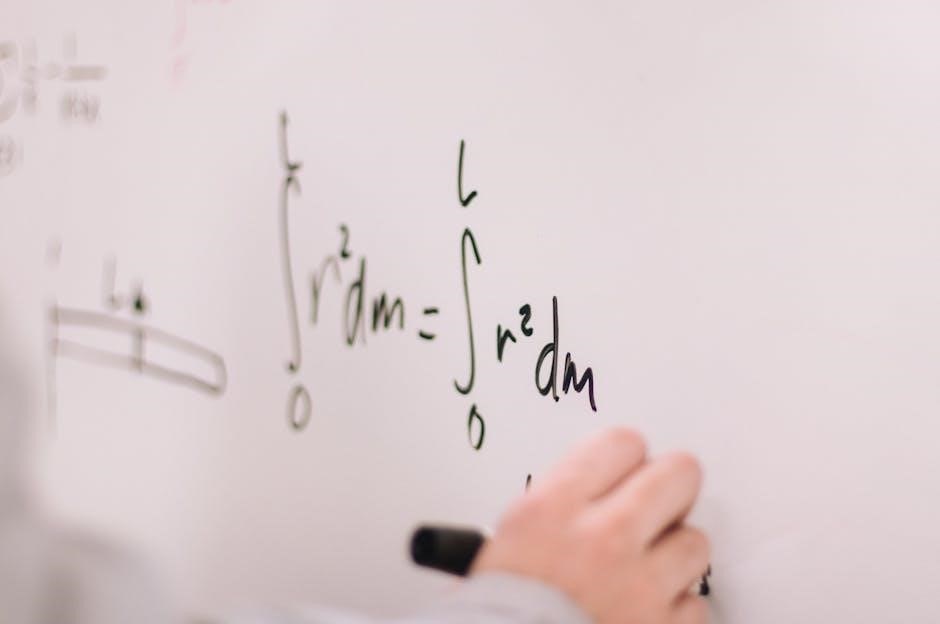
Step-by-Step Guide to Solving Two-Step Equations
Master solving two-step equations by identifying operations, applying inverses, and isolating variables. Practice with worksheets and answers to build confidence and accuracy in your solutions.
3.1 Identifying the Operations Involved
Identifying the operations involved is the first step in solving two-step equations. Start by carefully reading the equation to determine which operations (addition, subtraction, multiplication, or division) are present. For example, in the equation 3x + 5 = 11, the operations are multiplication (3x) and addition (+5). Similarly, in 7 – 2y = 3, the operations are subtraction (-2y) and subtraction (7). Once you identify the operations, you can plan the inverse operations needed to isolate the variable. This step ensures clarity and helps in applying the correct sequence of steps to solve the equation effectively.
3.2 Applying Inverse Operations to Isolate the Variable
Applying inverse operations is a critical step in solving two-step equations. Inverse operations “undo” the original operations, helping to isolate the variable. For example, if an equation involves addition and multiplication, you would first subtract to reverse the addition, then divide to reverse the multiplication. Always perform inverse operations in the reverse order of operations (PEMDAS/BODMAS). This ensures the variable is isolated on one side of the equation. Practice worksheets with answers can help you master this process, as they provide clear examples and solutions to common problems. Regular practice strengthens your ability to apply inverse operations effectively and solve equations accurately.
3.3 Checking the Solution
After solving a two-step equation, it’s essential to check your solution to ensure accuracy. Substitute the value back into the original equation and simplify both sides. If both sides are equal, your solution is correct. This step helps verify that no mistakes were made during the solving process. For example, if you solved for ( x ) and found ( x = 5 ), replace ( x ) with 5 in the original equation and confirm that both sides balance. This verification process reinforces understanding and builds confidence in your problem-solving skills. Always remember, checking your work is a crucial part of mastering two-step equations.

Common Challenges in Solving Two-Step Equations
Dealing with negative numbers, managing multiple operations, and avoiding common mistakes are key challenges. These obstacles can hinder problem-solving skills, but practice with worksheets can build confidence and accuracy.
4.1 Dealing with Negative Numbers
Negative numbers can add complexity to two-step equations, requiring careful attention to signs. When solving, remember that subtracting a negative is like adding a positive, and vice versa. For example, in the equation ( x – (-3) = 5 ), the negative sign before the 3 changes the operation to addition, making it ( x + 3 = 5 ). Always keep track of negative signs during each step to avoid errors. Practicing with worksheets can help build confidence in handling negative numbers effectively. Regular review of these concepts ensures mastery and reduces common mistakes, such as misapplying inverse operations or miscalculating signs.
4.2 Managing Multiple Operations
Managing multiple operations in two-step equations requires careful attention to the order of operations and their inverses. Start by identifying the operations applied to the variable, such as multiplication and addition. To isolate the variable, perform the inverse operations in the reverse order. For example, in the equation (3x + 5 = 11), first subtract 5 from both sides to eliminate the constant term, resulting in (3x = 6). Then, divide both sides by 3 to solve for (x), yielding (x = 2). Always check your solution by substituting it back into the original equation to ensure accuracy. This method ensures clarity and helps avoid common mistakes when dealing with multiple operations.
4.3 Avoiding Common Mistakes
When solving two-step equations, common mistakes often arise from rushing through steps or misapplying operations. Forgetting to apply the order of operations or incorrectly using inverse operations are frequent errors. Additionally, mishandling negative numbers and not simplifying expressions properly can lead to incorrect solutions. To avoid these pitfalls, work methodically, double-check each step, and ensure operations are applied correctly. Always verify your solution by substituting it back into the original equation. Practicing regularly and reviewing mistakes will help build accuracy and confidence in solving two-step equations effectively.
Practice Worksheets for Two-Step Equations

Explore a variety of practice worksheets designed to enhance your skills in solving two-step equations. These resources, available in PDF formats, offer step-by-step solutions and exercises to improve problem-solving abilities.
5.1 Types of Worksheets Available
Various types of worksheets are available to practice solving two-step equations, catering to different learning needs. These include basic practice sheets, mixed-operation worksheets, word problem-focused exercises, and timed drills. Some worksheets incorporate visual aids, while others offer step-by-step guidance. Advanced sheets may combine two-step equations with real-world scenarios or multiple-step problems. Additionally, worksheets with answers provide immediate feedback, helping learners assess their progress. Interactive PDF versions are also popular, offering a convenient and organized way to practice. Whether you’re a beginner or looking to refine your skills, there’s a worksheet type to suit your learning style and goals.
5.2 Benefits of Using Worksheets
Using worksheets for solving two-step equations offers numerous benefits. They provide structured practice, helping students master algebraic concepts at their own pace. Worksheets identify knowledge gaps, allowing targeted improvement. Regular use enhances problem-solving skills and builds confidence. They also serve as valuable resources for homework or revision. With answers included, students can self-assess and learn from mistakes. Worksheets cater to different learning styles, making math engaging and accessible. By reinforcing step-by-step problem-solving, they prepare learners for more complex equations. Overall, worksheets are an essential tool for developing proficiency in two-step equations and fostering a strong foundation in algebra.
5.3 How to Effectively Use Worksheets
To maximize learning, start with simpler problems and gradually move to more complex ones. Use the answer key to check your work and understand mistakes. Time yourself to improve speed and accuracy. Review incorrect answers to identify common errors and avoid them in future. Practice regularly to build confidence and fluency in solving two-step equations. Incorporate real-world examples to apply skills practically. Collaborate with peers or teachers to discuss challenging problems. Track progress over time to measure improvement. By following these steps, worksheets become a powerful tool for mastering two-step equations and strengthening overall math proficiency.
Solving Two-Step Equations with Answers
6.1 Understanding the Answer Key
Mastering two-step equations involves using inverse operations to isolate variables. Worksheets with answers provide clear solutions, helping you verify your work and improve problem-solving skills effectively.
6.1 Understanding the Answer Key
The answer key is an essential tool for verifying solutions to two-step equations. It provides correct answers, enabling students to check their work and identify mistakes. By comparing their solutions to the key, learners can ensure accuracy and understand where errors occurred. This resource is particularly useful for self-study, as it offers immediate feedback. The answer key also helps reinforce concepts by confirming proper application of inverse operations and order of operations. Regular use of the answer key fosters confidence and improves problem-solving skills, ensuring mastery of two-step equations. It serves as a valuable companion to the worksheet, promoting effective learning and retention of mathematical principles.
6.2 Learning from Mistakes
Mistakes are an inevitable part of the learning process when solving two-step equations. Analyzing errors helps identify common pitfalls, such as miscalculations or misapplying inverse operations. By reviewing incorrect answers, students can pinpoint where they went wrong and understand the correct approach. For instance, forgetting to distribute a negative sign or reversing the order of operations are frequent errors. Using the provided answer key, learners can compare their work and gain insights into proper problem-solving techniques. This reflective process enhances understanding and builds confidence. Emphasizing the “why” behind each step ensures a stronger grasp of mathematical concepts, fostering long-term mastery rather than temporary solutions.
6.3 Using Answers to Improve Skills
Utilizing the answer key provided in the worksheet is a powerful way to enhance your understanding and mastery of two-step equations. By comparing your solutions to the correct answers, you can identify areas where you may have made mistakes and learn from them. This process helps reinforce the concepts and strategies taught in the worksheet. Regularly reviewing the answers allows you to track your progress and build confidence in solving equations. Over time, this practice will improve your problem-solving skills and ensure a strong foundation in algebra. Consistent use of the answer key will guide you toward mastering two-step equations effectively.
Real-World Applications of Two-Step Equations
Two-step equations are essential in science for calculating distances, in finance for budgeting, and in everyday tasks like cooking or planning events, making them practical problem-solving tools.
7.1 Science and Technology
In science and technology, two-step equations are invaluable for solving real-world problems. For instance, in physics, calculating distance involves multiplying speed by time, then adding initial distance. In chemistry, balancing equations often requires solving for unknown quantities using two operations. Engineers use two-step equations to design systems, ensuring safety and efficiency. These equations also aid in data analysis, helping scientists interpret experimental results accurately. By mastering two-step equations, students gain essential skills for future careers in STEM fields, where problem-solving is critical. Regular practice with worksheets enhances proficiency, making complex calculations more manageable. Embrace these exercises to excel in science and technology applications.
7.2 Finance and Budgeting
In finance and budgeting, two-step equations are invaluable for managing personal or business funds. For instance, calculating total expenses after taxes or determining savings rates involves multiple operations. Suppose you earn $500 weekly and save 20% after a 10% tax deduction. First, calculate the tax: $500 * 0.10 = $50. Then, subtract the tax and calculate savings: ($500 – $50) * 0.20 = $90. This practical application helps individuals allocate resources efficiently, ensuring financial stability. By mastering two-step equations, you can make informed decisions about budgeting, investments, and long-term financial planning, making math a powerful tool for real-world success.
7.3 Everyday Problem-Solving
Two-step equations are invaluable in everyday problem-solving, helping individuals manage tasks like budgeting, cooking, and planning. For instance, calculating the total cost of groceries after discounts or adjusting recipe ingredients involves multiple operations, mirroring two-step equations. These equations also aid in scheduling, such as determining travel time with stops or calculating savings goals. By mastering two-step equations, one can efficiently tackle real-world challenges, enhancing their ability to organize and balance resources. This practical application underscores the importance of these equations in maintaining order and efficiency in daily life, making them a cornerstone of both academic and real-world problem-solving skills.

Tips for Mastering Two-Step Equations
To master two-step equations, practice regularly, understand inverse operations, check your solutions, break down problems, and seek help when needed. Consistency and patience are key.
8.1 Building a Strong Foundation in Basic Math
A strong foundation in basic math is crucial for mastering two-step equations. Understanding numbers, operations, and their inverses is essential. For instance, learning to trace and recognize the number 2, as seen in educational videos, helps build number sense. Counting and simple arithmetic skills, like adding two mittens or understanding idioms involving the number two, lay the groundwork for algebra. Practicing these fundamentals ensures a smooth transition to solving equations. Without a solid base, even simple equations can become challenging. Therefore, dedicating time to basic math concepts is vital for long-term success in algebra and beyond.
8.2 Practicing Regularly
Regular practice is essential for mastering two-step equations. Consistent effort helps build confidence and fluency in solving problems. Start with simple equations and gradually move to more complex ones. Use worksheets with answers to track your progress and identify areas needing improvement. Dedicate a specific time each day for practice to develop a routine. Begin with problems involving basic operations and slowly incorporate multiple operations. Utilize online resources or textbooks for varied exercises. Reviewing mistakes and understanding where you went wrong is crucial for improvement. Over time, regular practice will make solving two-step equations second nature, enhancing your overall math skills.
8.3 Seeking Help When Needed
Seeking help when needed is crucial for mastering two-step equations. Don’t hesitate to ask teachers, classmates, or tutors for clarification on challenging problems. Utilize online resources, such as educational videos or forums, to supplement your learning. Worksheets with answers can also guide you in understanding where you might be going wrong. Remember, asking for help is a sign of determination to improve. By addressing difficulties early, you can build a stronger foundation in algebra and problem-solving. Embrace opportunities to learn from others and use available tools to enhance your skills. Seeking help is a proactive step toward success in math and beyond.
Conclusion
Mastering two-step equations is crucial for algebraic proficiency. Regular practice with worksheets enhances problem-solving skills, fostering confidence in tackling complex math challenges effectively and efficiently always.

9.1 Summary of Key Points
In summary, two-step equations are essential for developing algebraic problem-solving skills. They involve performing two operations to isolate the variable, such as addition, subtraction, multiplication, or division. Understanding inverse operations and the order of operations is crucial for accuracy. Regular practice with worksheets, especially those with answers, helps build confidence and mastery. Real-world applications in finance, science, and everyday situations highlight their importance. By following a systematic approach—identifying operations, applying inverses, and checking solutions—students can overcome challenges and achieve proficiency. Consistent practice and reviewing mistakes are key to long-term success in solving two-step equations.
9.2 Encouragement for Further Practice
Consistent practice is key to mastering two-step equations. By dedicating time to solve worksheets, you’ll build confidence and improve problem-solving skills. Use the provided answer keys to check your work and learn from mistakes. Remember, every correct answer brings you closer to mastery. Embrace challenges and celebrate progress, no matter how small. The more you practice, the more intuitive solving equations will become. Stay motivated, and soon you’ll excel in tackling even complex problems with ease. Keep pushing forward—your efforts will pay off!
9.3 Final Thoughts on the Importance of Mastery
Mastery of two-step equations is crucial for algebraic proficiency and real-world problem-solving. Just as the number two represents a fundamental step in counting, these equations form a cornerstone in mathematical reasoning. Consistent practice with worksheets enhances problem-solving skills, essential in science, finance, and everyday situations. Embrace challenges, learn from mistakes, and recognize the value of persistence in achieving math fluency.
